求详解！！！！！！！

高中数学，求详解！！！！！！！

第一题。分母的被开方式【是一个只可以 在x轴上方的 开口向下的 抛物线 的 一段】。 所以，-3≤x≤-1，就是原题目的单调（减）区间；那么-1≤x≤1，就是单调（增）区间。 第二题。以1/2为底的对数函数是【减函数】。真数是【开口向下的抛物线（大于0）的一段】。 （因为负数和0无对数）。以顶点的两侧来区分就可以啦。注意“减减为增，减增为减”。 第三题。真数必须大于1。于是原函数的定义域就是（1，+无穷）。 但是直线y=x的增长速度很快，是直线型的，而对数函数的增长速度逐渐变慢，于是两个相减，就得到原函数的单调（增）区间是（1，+无穷）。

高中数学，求详解！！！！！！！！

1) 令ωx+φ=kπ，解出x=(kπ-φ)/ω，那么可以写出函数的零点坐标：设M(-φ/ω，0)，那么N((π-φ)/ω，0)，令ωx+φ=π/2+2kπ，解出x=(π/2+2kπ-φ)/ω,那么可以写出函数的最大值点坐标：设D((π/2-φ)/ω,A)，那么C((3π/2-φ)/ω，-A)，又F为MD的中点，那么0=-φ/ω+(π/2-φ)/ω，2=0+A,解出A=2,φ=π/4.△CDM的面积S等于△DMN的面积S1加上△CMN的面积S2，而S1=1/2*π/ω*2=π/ω，S2=1/2*1/2*π/ω*2=π/ω，所以S=S1+S2=2π/ω=2π/3,解出ω=3。综上可以求出函数f(

数学题，求详解！！！！！

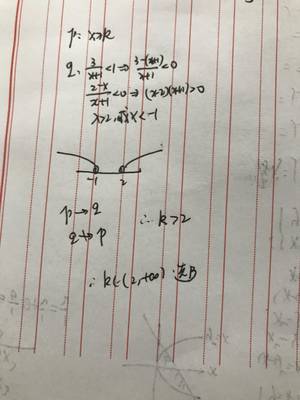
详细过程如图rt……先要判断充分不必要条件满足的情况，再就是注意不能取等号2，希望能帮到你解决问题

数学题！求详解！！！

解：14、y=sinx+cosx+sinxcosx 设t=sinx+cosx，sinxcosx=（t^2-1）/2 t=√2sin（x+丌/4）∴-√2≤t≤√2 y=t+（t^2-1）/2=1/2×（t+1）^2-1 ∵t=-1∈[-√2，√2] ∴当t=-1时，即y最小值=-1 ∵√2-（-1）>-1-（-√2） ∴当t=√2时，y最大值=√2+1/2 15、tan乄=2 （1）原式=（sin乄+cos乄）/cos乄/（sin乄-cos乄）/cos乄 =（tan乄+1）/（tan乄-1） =（2+1）/（2-1）=3 （2）原式=（1+cos2乄）/2+sin2乄+1 =1/2×cos2乄

求详解！！！！

(1)第一问不要用牛顿定律，用动能定理解，A为初位置，C为末位置，库仑力做正功，摩擦力和重力做负功，初动能为0。 二分之一mv^2=8*1.5（库仑力作用下对地的位移）-1*1-mgh 解得v=10m/s (2)C为初位置，类比竖直上抛做。库仑力仍为8牛，即压力为8牛，摩擦力为0.5*8=4牛，方向向下，重力为2牛，方向向下，合力为10牛。加速度为50m/s^2,初速度为10，末速度为0，则位移为1m,之后摩擦力变为静摩擦（因为动摩擦里力4牛大于重力2牛），物体静止。即物体停在C点上方1m处。